Block Designs
We have seen lots of symmetry in lots of different families. Families of chords that derive from the same scale, families of chords with the same adjacent intervals, families of chords where the sums of their notes are the same, families where the chords are all the same Forte set, families of homometric pairs, and so on. The members of the families were all equal in one sense or another, the families were complete, and the similarities and differences were always reflecting one anoth- er. But there is even more symmetry in combinatorial designs or block designs, and this is very different because it doesn’t have anything to do with acoustical characteristics, but rather with abstract mathematical relationships. As you will see, the elements of a block design have equality in very precise and exact ways, and completeness is essential before one can even get started.
With block designs all acoustical characteristics are essentially forgotten. No more overtone series, no more ideas of consonance and dissonance, and no more octave equivalence. In the real world octaves never were equal, or even equivalent, and in fact, one hears a rather great difference between any note and the same note an octave higher. Accepting the convention of octave equivalence was reasonable for music theorists from Rameau to Forte, and this convention worked fine for the music they studied. A chord was a chord, and it didn’t really matter what octaves the notes fell into, though it was better not to mess around with the bass note. But we have seen that the height of a chord, the value of that height modulo something, and the distribution of adjacent intervals are also important characteristics and need to be considered if we wish to go further into harmony, and now we are moving into a world where even these things are not directly relevant. Block designs come from an abstract mathematical world, rather a long ways from the acoustical world. Scales are no longer scales but rather sets. Chords are no longer chords but rather subsets. Notes are no longer notes but rather elements. Music theory is now replaced by group theory, though we can make music all the same.(...)
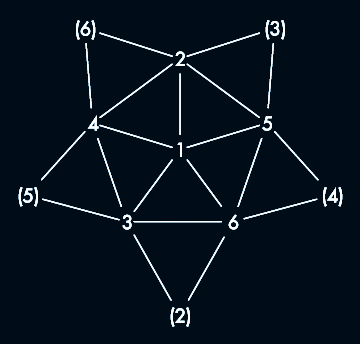
Block design (6,3,2) as a complete graph, where each node has 5 edges
